E - Loi exponentielle

Durée de vie sans vieillissement

Une loi exponentielle modélise la durée de vie d'un phénomène sans mémoire ou sans vieillissement ou sans usure.

La probabilité que le phénomène dure un temps $t+s$ sachant qu'il a duré $t$ est égale à la probabilité qu'il dure un temps $s$. Ainsi, si $X$ est une variable aléatoire qui suit une loi exponentielle, alors :

$P_{X\geqslant t}(X\geqslant t+s)=P(X\geqslant s)$

Cette modélisation est par exemple utilisée :

• pour la désintégration radioactive d'atomes

• pour la durée de vie de composants électroniques

• la durée de vie d'une ampoule à LED

Loi exponentielle

On démontre que si une variable aléatoire $X$ suit une loi exponentielle, alors il existe un paramètre $\lambda>0$ tel que sa densité, définie sur $[0\;;\;+\infty[$, est donnée par :

$f(x)=\lambda e^{-\lambda x}$

Ainsi, pour $0\leqslant a\leqslant b$,

$P(a\leqslant X\leqslant b)=\int_a^b\lambda e^{-\lambda x}\,\text{d}x$

On note alors

$X\sim E(\lambda)$

Proposition

Pour $0\leqslant a\leqslant b$,

• $P(a\leqslant X\leqslant b)=e^{-\lambda a}-e^{-\lambda b}$
• $P(X\leqslant b)=1-e^{-\lambda b}$
• $P(a\leqslant X)=e^{-\lambda a}$

Exemple

loi-expo.png

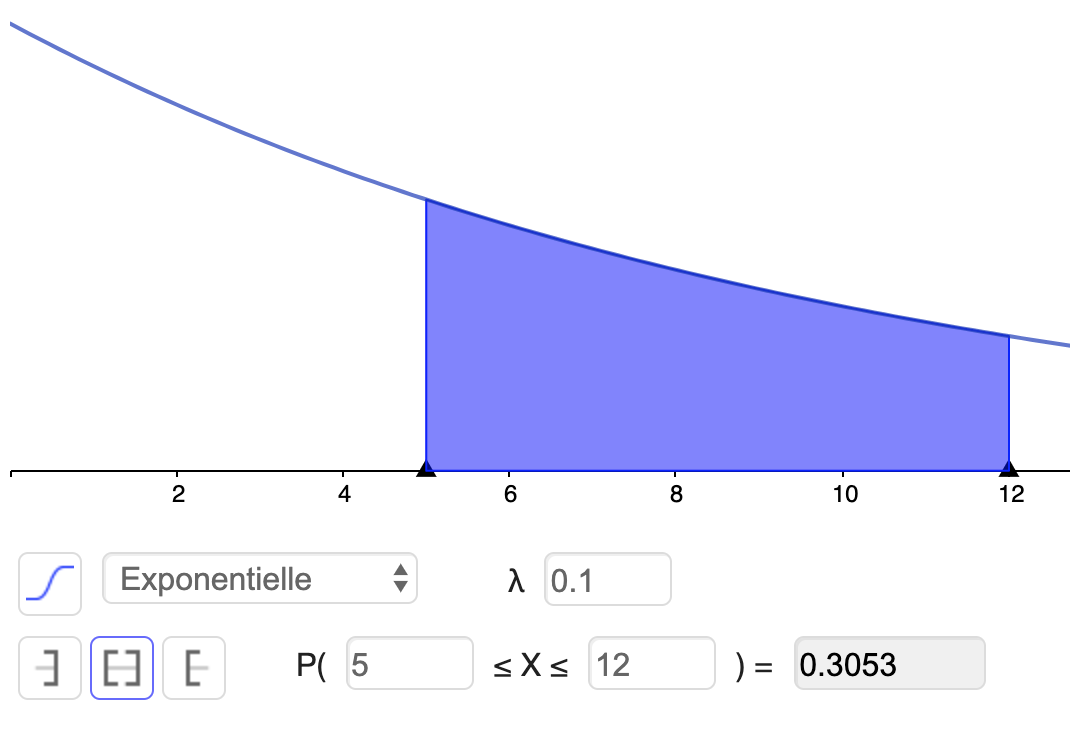
• Soit $X\sim E(0.1)$, calculer :

  • $P(5\leqslant X\leqslant 12)$
  • $P(X>10)$
  • $P(x\leqslant 3)$

expo-numworks.png

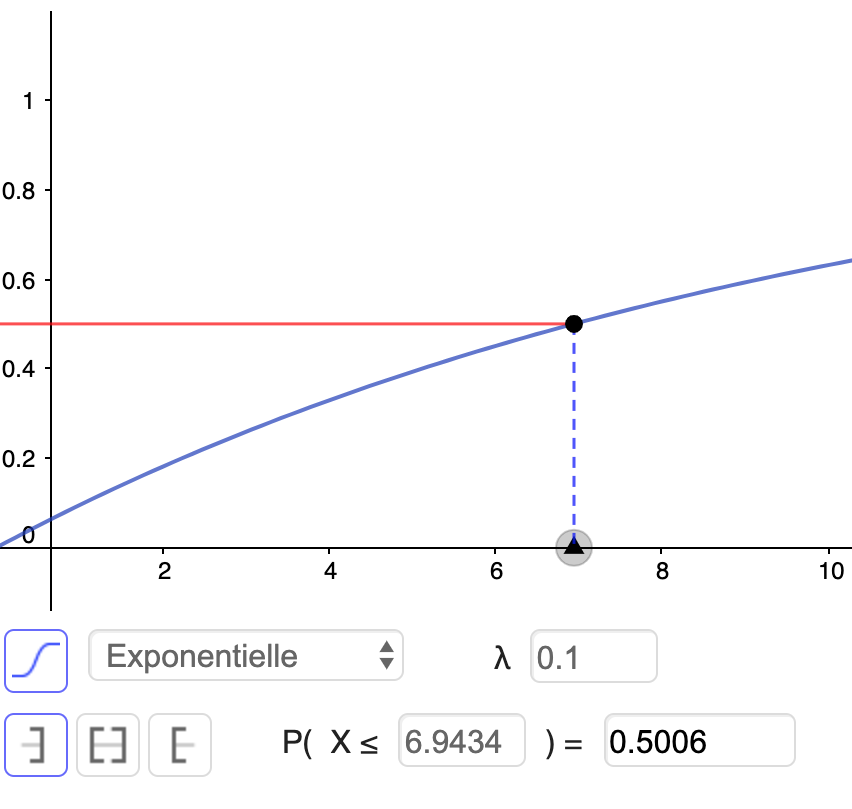
Fonction de répartition et Demi-vie

La fonction de répartition d'une variable aléatoire $X\sim E(\lambda)$ est donnée par : $F:t\mapsto P(X\leqslant t)=1-e^{-\lambda t}$

Si on dispose d'un stock de composants suivants tous une même loi exponentielle, alors on peut interpréter $F(t)$ comme la proportion du stock encore présent jusqu'à $t$.

La demi-vie $t_{\text{demi-vie}}$ d'un composant est la médiane de sa durée de vie , c'est-à-dire la durée en deçà de laquelle il reste 50 % d'un stock de ce composant.

$P(X\leqslant t_{\text{demi-vie}})=0,5$

demi-vie.png

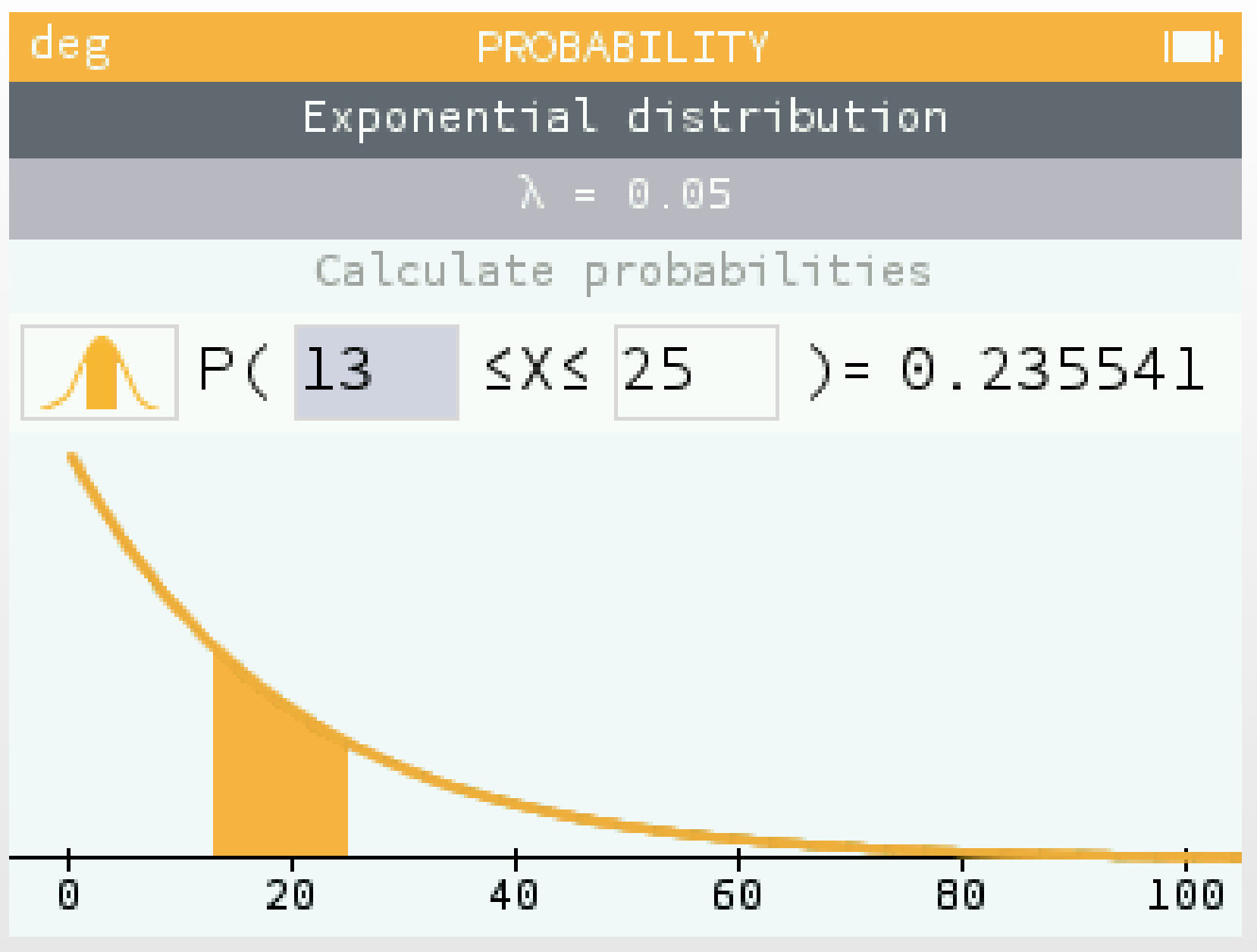
Exemple

Le plutonium 238 est un élément radioactif qui suit une loi exponentielle.

Il possède une demi-vie de 88 ans :

• dans un stock de plutonium 238, en raison de sa radioactivité, la moitié du stock s'est désintégré, au bout de 88 ans.

• un atome de plutonium 238 a une chance sur deux de s'être désintégrer au bout de 88 ans.

• Déterminer le paramètre $\lambda$ de la loi exponentielle suivie par le plutonium 238 au millième près.
• Quelle est la probabilité pour qu'un atome de plutonium 238 se désintègre entre ses 60 et 100 ans ?

• Quelle est la probabilité pour qu'un atome de plutonium 238 se désintègre après 150 ans ?

• Calculer l'espérance de vie du plutonium 238 donnée par $E(X)=\int_0^{+\infty}\lambda xe^{-\lambda x}\,\text{d}x$

Proposition

$X$ suit une loi exponentielle de paramètre $\lambda>0$ $X\sim E(\lambda)$

• Espérance de vie $\qquad E(X)=\dfrac{1}{\lambda}$
• Demi-vie $\qquad t_{\text{demi-vie}}=\dfrac{\ln(2)}{\lambda}=\ln(2)\times E(X)$
• Écart-type $\qquad \sigma(X)=\dfrac{1}{\lambda}$

Exercices 8 à 12 pages 379-380