2. Calcul matriciel #1

Chasse au trésor !

155KB

BTS SN-TP18-ALG-Etude d'un graphe.pdf

pdf

Un problème de chemins

En partant d'une carte au trésor :

carte-au-tresor.jpg

On construit un graphe contient trois points A, B et C reliés par des chemins de la façon suivante :

graph2.png

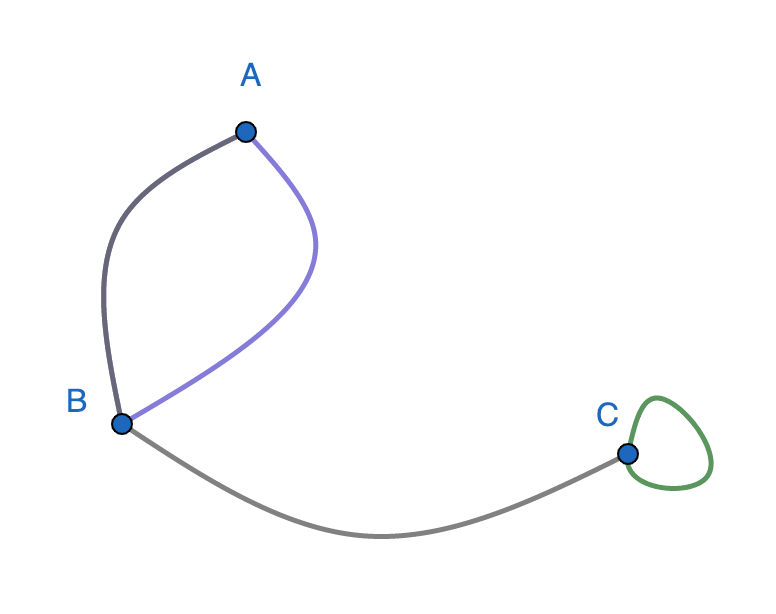
1. Combien y a-t-il de chemins qui permettent de passer de A à B en un tronçon ? de B à C ? de A à C ? de C à C ?

2. Remplir le tableau suivant en indiquant le nombre de chemins d'un seul tronçon reliant les points deux à deux :

   $T_1=\left[\begin{array}{cccc}&A&B&C\\A&\cdots&\cdots&\cdots\\B&\cdots&\cdots&\cdots\\C&\cdots&\cdots&\cdots\\\end{array}\right]$
3. La matrice d'adjacence du graphe est obtenue en ne gardant que les nombres :$M_1=\left(\begin{array}{ccc}\cdots&\cdots&\cdots\\\cdots&\cdots&\cdots\\\cdots&\cdots&\cdots\\\end{array}\right)$
4. Que remarque-t-on ?

5. Combien y a-t-il des chemins de deux tronçons qui relient A à C ? A à A ?

6. Remplir le tableau suivant en indiquant le nombre de chemins de deux tronçons reliant les points deux à deux : $T_2=\left[\begin{array}{cccc}&A&B&C\\A&\cdots&\cdots&\cdots\\B&\cdots&\cdots&\cdots\\C&\cdots&\cdots&\cdots\\\end{array}\right]$
7. En extrayant les nombres du tableau $T_2$ on obtient une nouvelle matrice :$M_2=\left(\begin{array}{ccc}\cdots&\cdots&\cdots\\\cdots&\cdots&\cdots\\\cdots&\cdots&\cdots\\\end{array}\right)$

Le nombre de chemins en deux tronçons pour joindre B à B correspond à la somme :

• du nombre de chemins en un tronçon de B à A multiplié par le nombre de chemins en un tronçon de A à B

• du nombre de chemins en un tronçon de B à B multiplié par le nombre de chemins en un tronçon de B à B

• du nombre de chemins en un tronçon de B à C multiplié par le nombre de chemins en un tronçon de C à B

Soit $2\times2+0\times0+1\times1$

• le nombre de chemins partants de $B$ vers les autres points sont donnés par la ligne 2 $\left(\begin{array}{ccc}2&0&1\\\end{array}\right)$
• le nombre de chemins depuis les autres points arrivants à $B$ sont donnés par la colonne 2 $\left(\begin{array}{c}2\\0\\1\\\end{array}\right)$
• On définit alors la "multiplication" d'une ligne par une colonne par la formule : $\left(\begin{array}{ccc}2&0&1\\\end{array}\right)^{\left(\begin{array}{c}2\\0\\1\\\end{array}\right)}=2\times2+0\times0+1\times1$

Application :

1. Multiplier la ligne 2 par la colonne 3

2. Que retrouve-t-on ?

Conséquence : on peut obtenir la matrice $M_2$ des trajets à 2 tronçons à l'aide d'un calcul sur la matrice $M_1$ des trajets à 1 tronçon.

Multiplication de deux matrices

Soit $A=\left(\begin{array}{ccc}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\\\end{array}\right)$ et $B=\left(\begin{array}{ccc}b_{1,1}&b_{1,2}&b_{1,3}\\b_{2,1}&b_{2,2}&b_{2,3}\\b_{3,1}&b_{3,2}&b_{3,3}\\\end{array}\right)$

On obtient alors la matrice produit

$A\times B=\left(\begin{array}{ccc}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\\\end{array}\right)^{\left(\begin{array}{ccc}b_{1,1}&b_{1,2}&b_{1,3}\\b_{2,1}&b_{2,2}&b_{2,3}\\b_{3,1}&b_{3,2}&b_{3,3}\\\end{array}\right)}=\left(\begin{array}{ccc}c_{1,1}&c_{1,2}&c_{1,3}\\c_{2,1}&c_{2,2}&c_{2,3}\\c_{3,1}&c_{3,2}&c_{3,3}\\\end{array}\right)$ où

$c_{i,j}=a_{i,1}\times b_{1,j}+a_{i,2}\times b_{2,j}+a_{i,3}\times b_{3,j}$

1. Calculer $M_1^2=M_1\times M_1$
2. Que retrouve-t-on ?

3. À l'aide de la calculatrice calculer $M_1^3$.
4. Que nous donne cette matrice $M_1^3$. Retrouver les résultats sur le graphe.