A - Loi binomiale

Variables aléatoires

Problème

Un jeu consiste à lancer un dé équilibré à 6 faces.

• Si le 6 sort le joueur perd 6 euros.

• Sinon le joueur gagne 1 euro.

Ce jeu est-il équitable ?

jeux-de-des.jpg

Définitions

On appelle expérience aléatoire, une expérience dont les résultats sont soumis au hasard. On note $\Omega$ l'ensemble des issues ou événements élémentaires de cette expérience aléatoire :

$\Omega =\{ e_1\;;\;e_2\;;\;e_3\;;\cdots;\;e_n\}$

On définit une variable aléatoire sur $\Omega$ lorsque l'on associe à chaque issue un nombre réel :

$X:e_i \mapsto x_i$

Si $X(\Omega)=\{ x_1\;;\;x_2\;;\;x_3\;;\cdots;\;x_n\}$ sont les valeurs prises par la variable aléatoire $X$, on obtient la loi de probabilité $X$ en donnant les probabilités $P(X=x_i)$ :

loi-proba-va.png

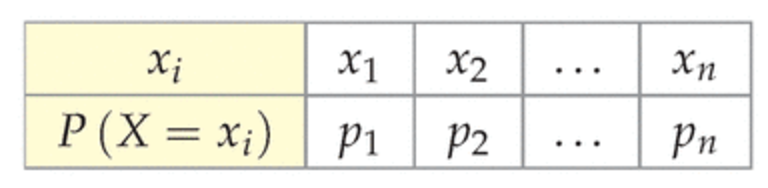
On a donc l'égalité : $P(X=x_1)+P(X=x_2)+\cdots + P(X=x_n)=1$

On appelle espérance de la variable aléatoire $X$ le réel :

$E(X)=p_1\times x_1+p_2\times x_2+\cdots +p_n\times x_n=\sum_{i=1}^n p_i\times x_i$

On appelle variance de la variable aléatoire $X$ le réel :

$V(X)=p_1\times (x_1-E(X))^2+p_2\times (x_2-E(X))^2+\cdots +p_n\times (x_n-E(X))^2$ ou de manière compactée et équivalente : $V(X)=\sum_{i=1}^n p_i\times (x_i-E(X))^2=\sum_{i=1}^n p_i\times x_i^2-E(X)^2$

On appelle écart-type de la variable aléatoire $X$ le réel :

$\sigma(X)=\sqrt{E(X)}$

Remarques :

• Un jeu est équitable si son espérance mathématique est nulle.

• La variance et l'écart-type donne des informations sur la distribution des valeurs prises par la variable aléatoire.

Exercice :

Une urne contient $5$ boules rouges, $3$ boules vertes et $2$ boules bleues. Un joueur tire au hasard une boule de l'urne ; si la boule tirée est bleue, le gain du joueur est de $10$ euros, si la boule est verte, le gain est de $5$ euros, si la boule est rouge, le joueur perd $8$ euros.

$X$ est la variable aléatoire qui compte le gain algébrique d'un joueur à l'issue d'une partie.

1. Déterminer la loi de probabilité de $X$ ;
2. Calculer l'espérance de $X$ ;
3. Calculer la variance de $X$ ;
4. Calculer l'écart-type de $X$ ;
5. Retrouver ces résultats à la calculatrice.

Exercices 1 à 4 page 333

Loi binomiale

Problème

On dispose d'une urne contenant 100 boules : 40 boules rouges et 60 boules noires. On effectue trois tirages successifs avec remise dans cette urne en notant à chaque fois la couleur obtenue.

• Qu'elle est la probabilité d'obtenir 3 boules rouges ?

• Qu'elle est la probabilité d'obtenir 1 boule rouge exactement sur les 3 tirages ?

• Qu'elle est la probabilité d'obtenir au moins une boule rouge sur les trois tirages ?

Sphère Loto.jpg

On note $X$ la variable aléatoire qui compte le nombre de boules rouges à l'issue des 3 tirages successifs avec remise.

• Donner $X(\Omega)$, l'ensemble des valeurs prises par $X$
• Remplir ce tableau :

$X(k)$	0	1	2	3
$P(X=k)$	...	...	...	...

• Construire le diagramme en bâton correspondant à ce tableau

Définitions

On appelle épreuve de Bernoulli de paramètre $p$ une expérience aléatoire à 2 issues, un succès et un échec :

• On note $S$, le succès de probabilité $P(S)=p$
• On note $\overline{S}$, le succès de probabilité $P(\overline{S})=1-p$

On appelle schéma de Bernoulli de paramètres $n$ et $p$ la répétition de manière identique et indépendante d'une épreuve de Bernoulli de paramètre $p$ :

$\to$ Construire un arbre illustrant un schéma de Bernoulli dans le cas $n=3$.

Combien y a-t-il dans cette arbre de branches contentant :

• aucun succès ?

• exactement 1 succès ?

• exactement 2 succès ?

• exactement 3 succès ?

Définition :

La variable aléatoire $X$ qui compte le nombre de succès à l'issue des $n$ répétitions identiques et indépendantes d'une épreuve de Bernoulli de paramètre $p$, suit une loi binomiale de paramètres $n$ et $p$ et est notée $\mathcal B(n\;;\;p)$. On note alors :

$X\sim\mathcal B(n\;;\;p)$

Exercices 5 page 333, 6, 7, 8 et 9 page 334

Théorème :

Si $X\sim\mathcal B(n\;;\;p)$ alors la loi de probabilité de $X$ est donnée par la formule :

$P(X=k)=\left( \begin{array}{c} n\\k \end{array} \right)p^k(1-p)^{n-k}$

avec $\left( \begin{array}{c} n\\k \end{array} \right)$, "$k$ parmi $n$" qui compte le nombre de choix de $k$ éléments parmi $n$.

Méthodes CALCULATRICE :

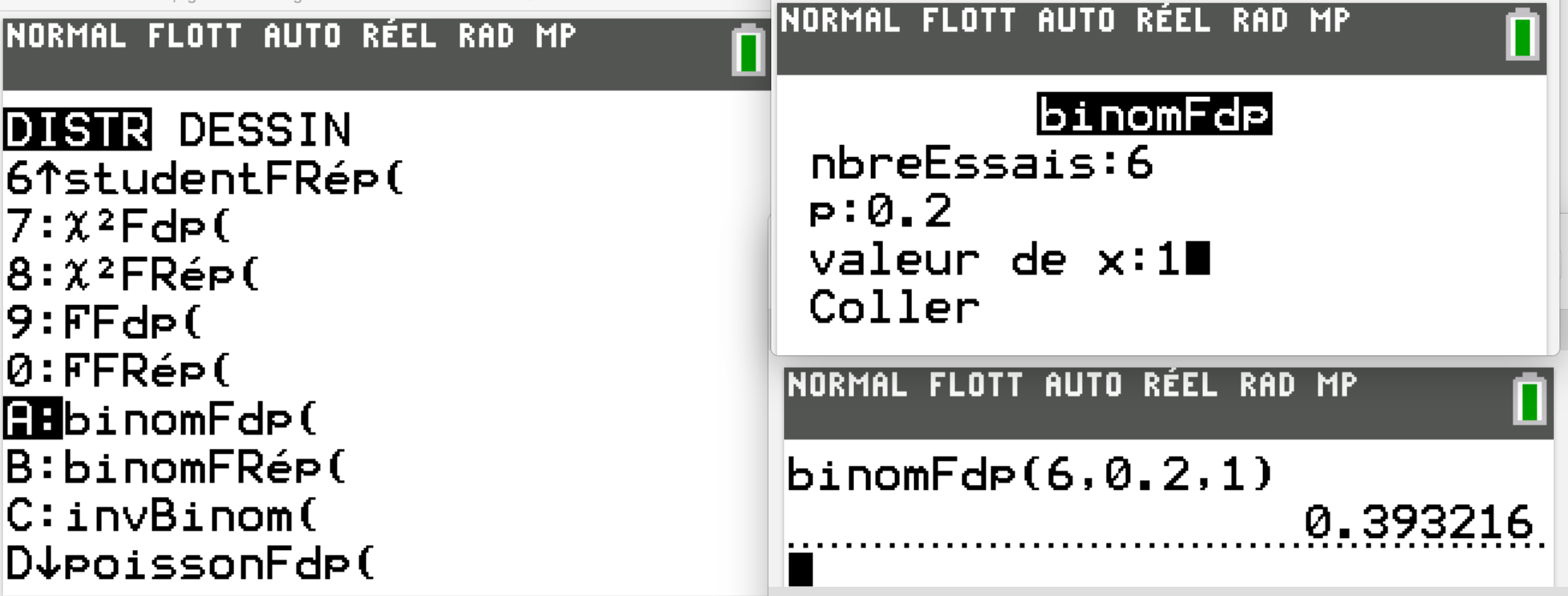
Retrouver à la calculatrice :

• Si $X\sim\mathcal B(6\;;\;0,2)$, $P(X=1)\approx 0,393216$
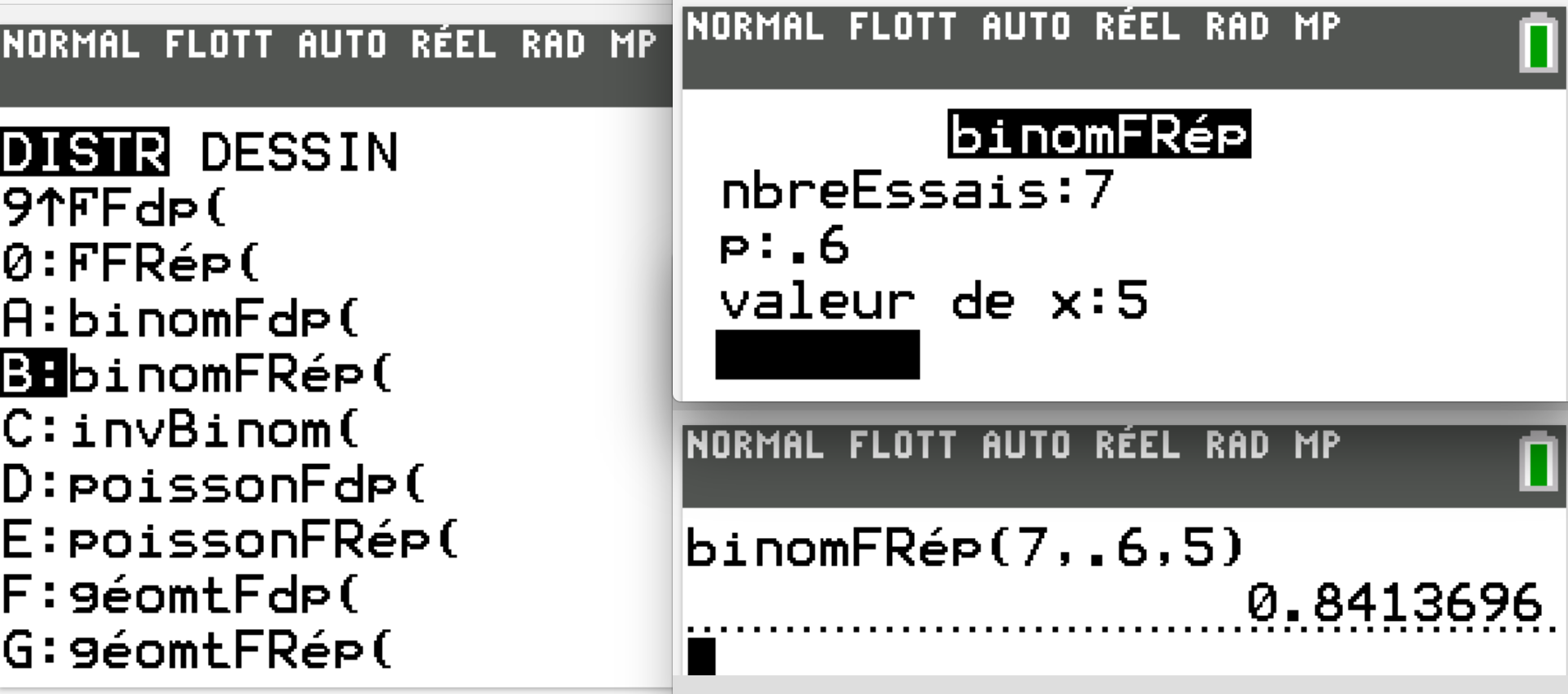
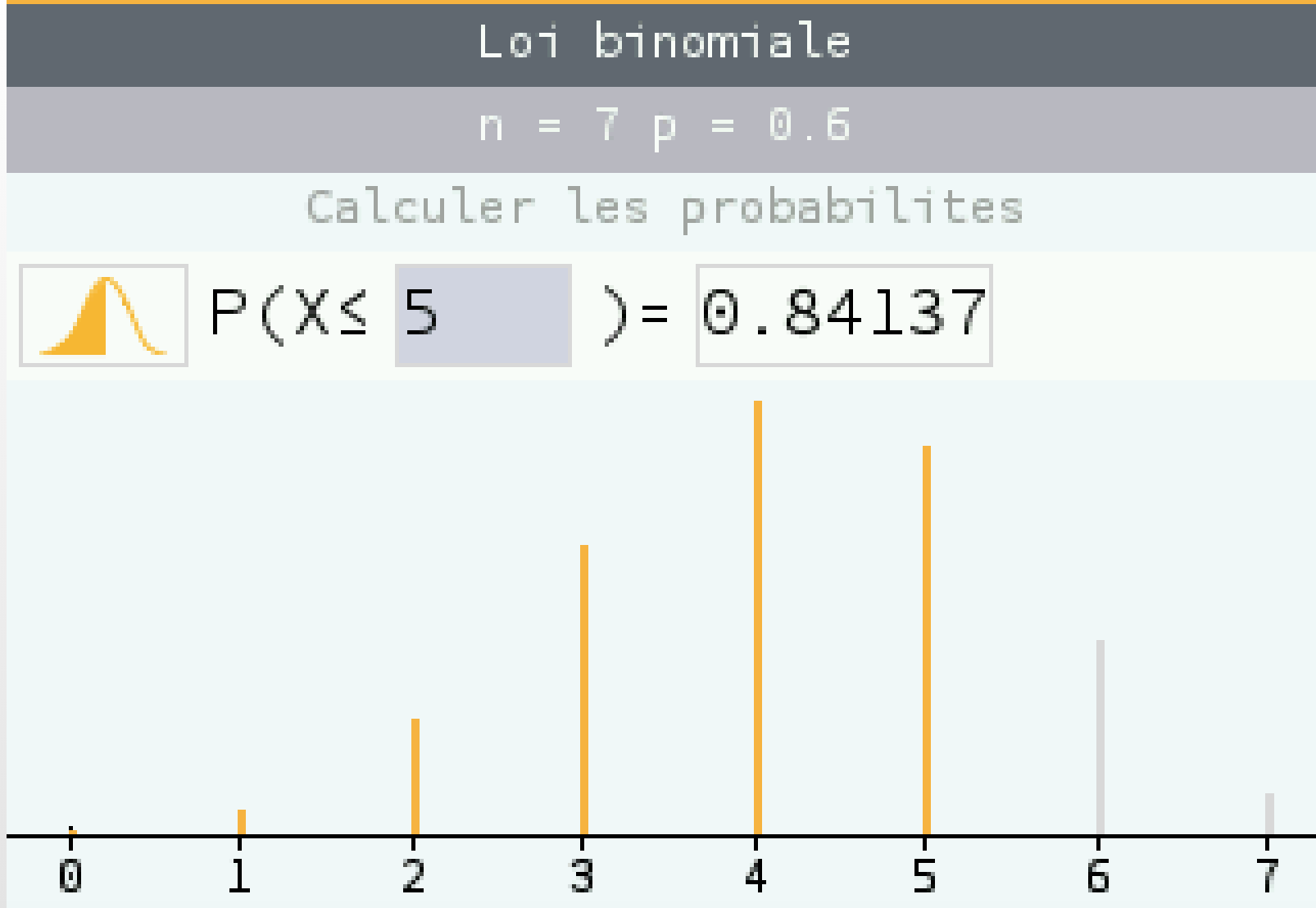
• Si $X\sim\mathcal B(7\;;\;0,6)$. $P(X\leqslant 5)\approx 0,8413696$

calc-binom.png

calc-binom-cum.png

binomiale-numworks.png

Exercices 9 à 13 page 334-335 Exercice 14 page 335

Propriétés :

Si $X\sim\mathcal B(n\;;\;p)$, alors :

• $E(X)=np$
• $V(X)=np(1-p)$
• $\sigma(X)=\sqrt{np(1-p)}$

Exercices 15 à 17 page 335

Synthèse : exercices 19 à 28 page 335-342