0. Dérivation (rappels)

Nombre dérivé

Définition

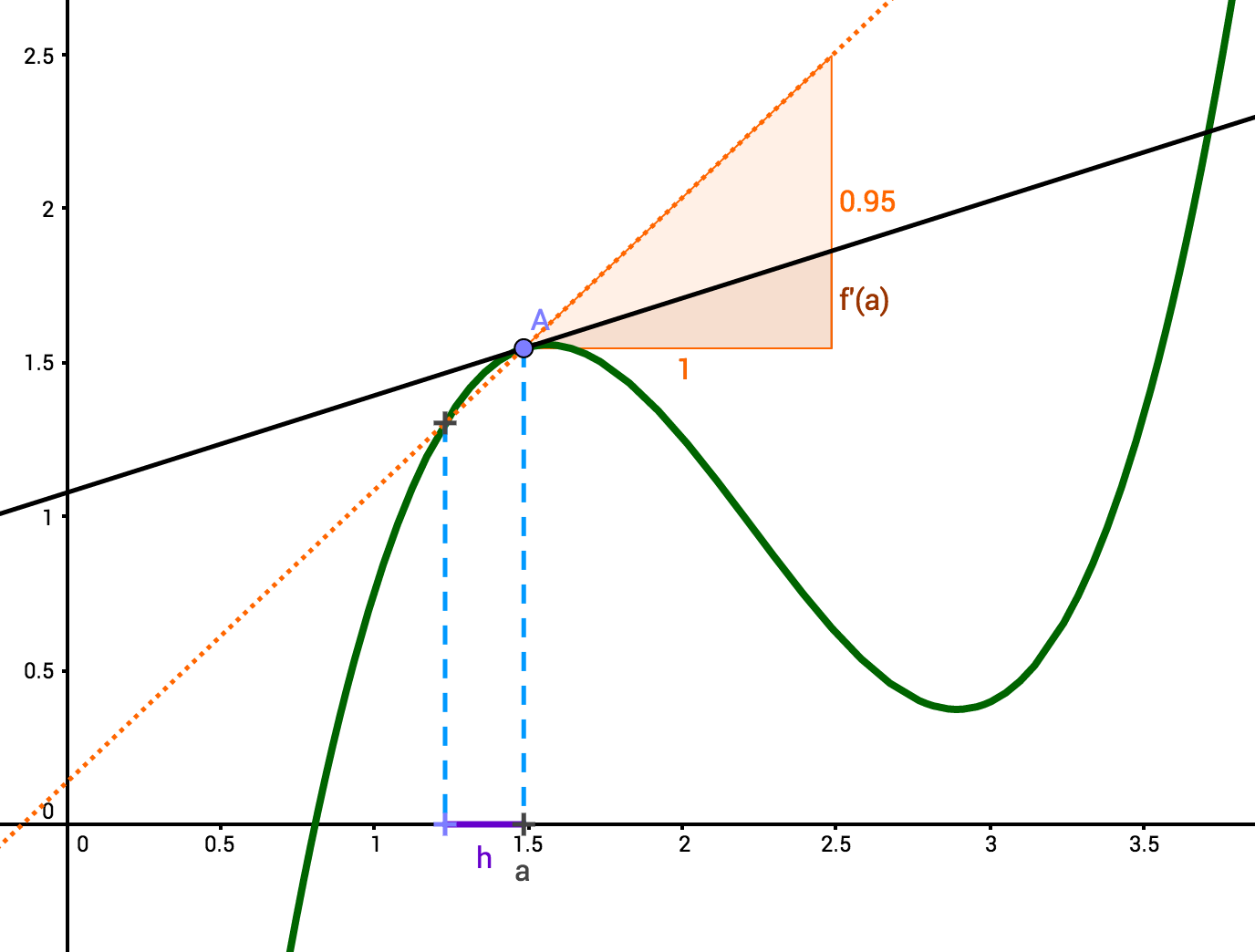
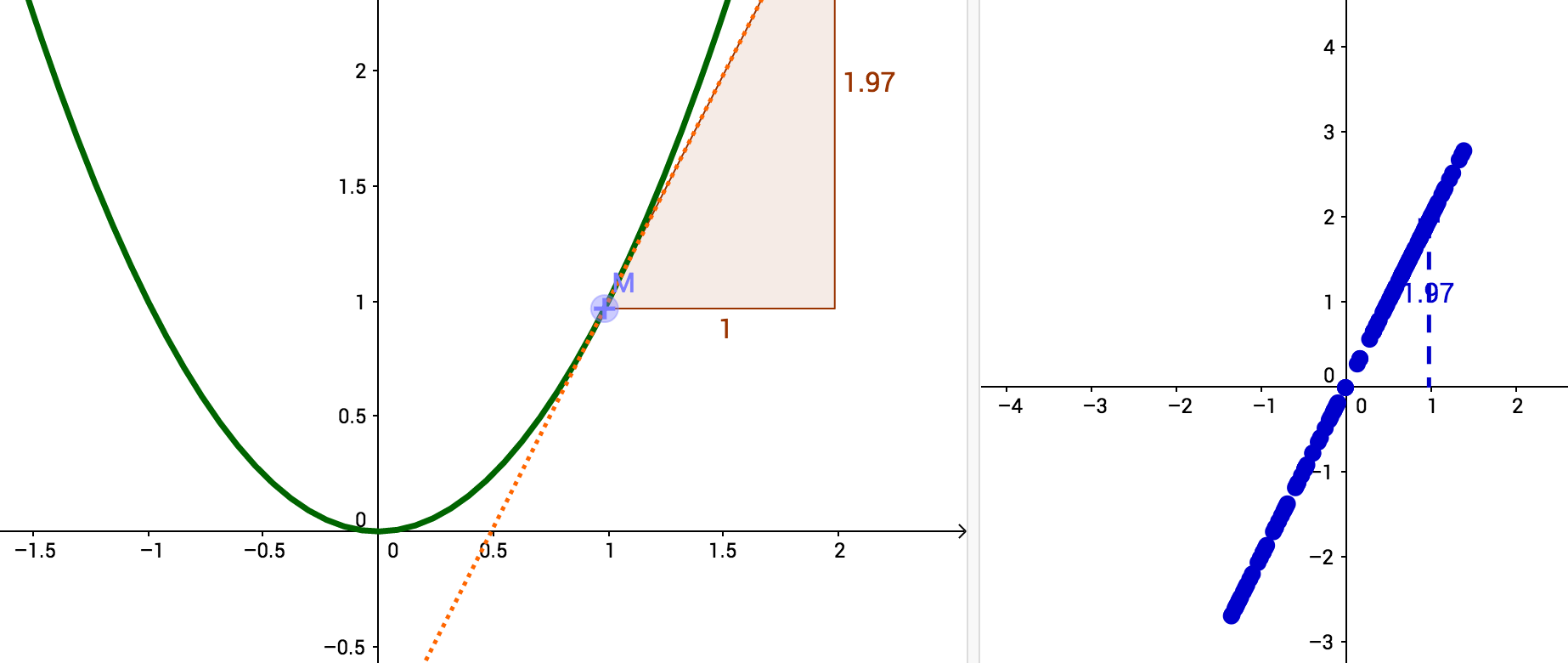
Soit $f$ une fonction définie sur un intervalle $I$, $a\in I$. On appelle taux d'accroissement de $f$ entre $a$ et $a+h$, où $h\in\mathbb{R}$, est le réel $\dfrac{f(a+h)-f(a)}{h}$

$f$ est dite dérivable en $a$ si le taux d'accroissement de $f$ entre $a$ et $a+h$ tend vers un réel $\ell$ lorsque $h$ tend vers $0$. On note alors $f'(a)=\lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h}=\ell$

Le réel $f'(a)$ est appelé nombre dérivé de $f$ en $a$.

Tangente

Proposition

Si $f$ est dérivable en $a$, alors $f'(a)$ est le coefficient directeur de la tangente à $\mathcal C_f$ au point d'abscisse $a$.

Proposition

Si $f$ est dérivable en $a$, alors $T_a : y = f'(a)\times (x-a) + f(a)$ est l'équation de la tangente à $\mathcal C_f$ au point d'abscisse $a$.

$\bigstar$ Illustration GeoGebra

tangente.png

$\clubsuit\,\clubsuit\,\clubsuit\;$ MÉTHODES

• Déterminer l'équation de la tangente à $f:x\mapsto x^2$ en 2 et en 0 ;
• Déterminer l'équation de la tangente à $h:x\mapsto \dfrac{1}{x}$ en 1 ;
• Déterminer l'équation de la tangente à $r:x\mapsto \sqrt{x}$ en 3.

Fonction dérivée

Définition

Soit $f$ une fonction définie sur un intervalle $I$. Si $f$ est dérivable en tout $x\in I$, alors on note $f'$ et on appelle fonction dérivée de $f$, la fonction définie sur $I$ par :

$f':x\mapsto f'(x)$

C'est la fonction qui a tout point $x$ de $I$ associe le coefficient directeur de la tangente à $\mathcal C_f$ au point d'abscisse $x$.

$\bigstar$ Illustration GeoGebra

derivée.png

Dérivée des fonctions usuelles

Fonction $f$	Fonction $f'$	$f$ définie sur	$f$ dérivable sur
$x\mapsto k$	$x\mapsto 0$	$\mathbb R$	$\mathbb R$
$x\mapsto m\times x+p$	$x\mapsto m$	$\mathbb R$	$\mathbb R$
$x\mapsto x^2$	$x\mapsto 2x$	$\mathbb R$	$\mathbb R$
$x\mapsto x^n$ avec $n\geqslant 2$	$x\mapsto n\times x^{n-1}$	$\mathbb R$	$\mathbb R$
$x\mapsto \dfrac{1}{x}$	$x\mapsto \dfrac{-1}{x^2}$	$\mathbb R-\{0\}$	$\mathbb R-\{0\}$
$x\mapsto \sqrt{x}$	$x\mapsto \dfrac{1}{2\sqrt{x}}$	$[0\;;\;+\infty[$	$]0\;;\;+\infty[$
$x\mapsto e^x$	$x\mapsto e^x$	$\mathbb R$	$\mathbb R$
$x\mapsto\ln x$	$x\mapsto \dfrac{1}{x}$	$]0\;;\;+\infty[$	$]0\;;\;+\infty[$
$x\mapsto\cos x$	$x\mapsto-\sin{x}$	$\mathbb R$	$\mathbb R$
$x\mapsto\sin{x}$	$x\mapsto\cos{x}$	$\mathbb R$	$\mathbb R$

Dérivées et opérations

Les formules indispensables pour pouvoir dériver quelques fonctions :

• La somme : $(u+v)'=u'+v'$
• Le produit : $(u\times v)'=u'\times v+u\times v'$
• L'inverse : $\left(\dfrac{1}{v}\right)'=\dfrac{-v'}{v^2}$
• Le quotient : $\left(\dfrac{u}{v}\right)'=\dfrac{u'v-uv'}{v^2}$
• Les puissances : $(u^n)'=n\times u^{n-1}\times u'$
• Les racines : $(\sqrt{u})'=\dfrac{u'}{2\sqrt{u}}$
• Exponentielle: $(e^u)'=u'\times e^u$
• Logarithme : $(\ln{u})'=\dfrac{u'}{u}$
• Fonctions circulaires : $(\cos{(ax+b)})'=-a\times\sin{(ax+b)}$ $(\sin(ax+b))'=a\times\cos(ax+b)$

Remarque : cas particulier du produit par une constante :

Si $k$ est un réel constant, on a $(k\times u)'=k\times u'$

$\clubsuit\,\clubsuit\,\clubsuit\;$ MÉTHODE :

Calculer les fonctions dérivées des fonctions suivantes :

• $f:x\mapsto x^3+\dfrac{1}{x}$
• $g:x\mapsto 7x^2$
• $h:x\mapsto x\sqrt{x}$
• $i:x\mapsto \dfrac{3}{x^2-7x+1}$
• $j:x\mapsto \dfrac{x-1}{x^2+1}$
• $k:x\mapsto (x^2+5)^3$
• $l:x\mapsto\ln(x^2+1)$
• $m:x\mapsto\sqrt{x^2+1}$
• $n:x\mapsto x^2e^{-3x}$

Problèmes et travaux pratiques

Problème 1

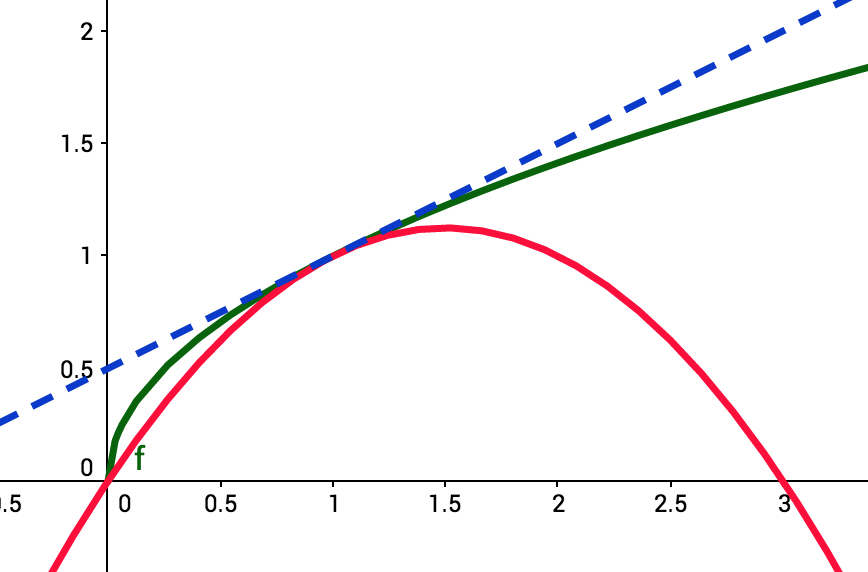
Soit $f(x)=\sqrt{x}$ et $g(x)=ax^2+bx$.

Déterminer $a$ et $b$ pour que ces deux fonctions possèdent la même tangente au point d'abscisse $1$.

tangente-commune.png

Problème 2

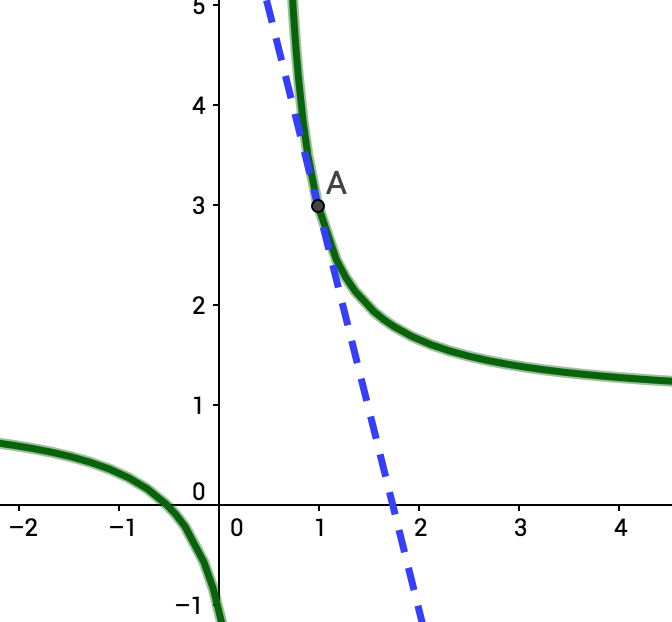
Soit $f(x)=\dfrac{2x+1}{2x-1}$.

Existe-t-il une autre tangente à $\mathcal C_f$ parallèle à la tangente $T_1$ à $\mathcal C_f$ au point d'abscisse $1$ ?

tangente-hyperbole.png

Variation et dérivation

Théorème fondamental #1

Soit $f$ une fonction définie et dérivable sur un intervalle $I$.

• $f$ est croissante sur $I$ si et seulement si $f'(x)\geqslant 0$ sur $I$
• $f$ est décroissante sur $I$ si et seulement si $f'(x)\leqslant 0$ sur $I$
• $f$ est constante sur $I$ si et seulement si $f'(x)= 0$ sur $I$

$\clubsuit\,\clubsuit\,\clubsuit\;$ MÉTHODE :

• Déterminer le sens de variation de $f:x\mapsto 2x^3+3x^2-36x$ sur $\mathbb{R}$
• Déterminer le sens de variation de $h:x\mapsto \dfrac{1}{x}+x$ sur $\mathbb{R^{+*}}$

Extremum d'un fonction

Théorème fondamental #2

Soit $f$ une fonction définie et dérivable sur un intervalle ouvert $I$.

• Si $f$ admet un extremum local (maximum ou minimum) en $a\in I$ alors $f'(a)=0$.
• Si la dérivée $f'$ s'annule en changeant de signe en $a\in I$, alors la fonction $f$ présente un extremum local (maximum ou minimum) en $a$.

Remarque : un intervalle ouvert est un intervalle du type $]c\;;\;d[$

1. Faire deux figures illustrant chacun des deux cas.

2. Pourquoi a-t-on pris soin d'être sur un intervalle ouvert $I$ ?
3. Pour la deuxième assertion, que peut-il se passer si $f'$ ne change pas de signe ? Illustrer.

Stricte monotonie

Une version plus précise du théorème #1 :

Soit $f$ une fonction définie et dérivable sur un intervalle $I$.

• Si $f'(x)>0$ sur $I$, alors $f$ est strictement croissante sur $I$
• Si $f'(x)<0$ sur $I$, alors $f$ est strictement décroissante sur $I$
• Si $f$ est strictement monotone sur $I$ alors $f'(x)$ est de signe constant et ne s'annule que de façon isolée.